Metamath: An Intro to “All of Mathematics”
How a simple proof validation engine was built from the ground up and without anything beyond a variable substitution scheme handles many fields of mathematics.

2020 was a rough year for many of us. With many jobs affected by the COVID-19 lockdown, there was a hole in many of our lives as we sought to connect with others. My personal pandemic project was to translate the logic of Gottlob Frege’s Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens (1879)1 to modern mathematical language, and hopefully patching the holes in the logic common to the use of Naive Set Theory2 prior to the turn-of-the-century revolution3 of Russell’s Paradox and the development of Axiomatic Set Theory4.
This seemed to be compatible with the goals of the Metamath project5 which in many ways is a successor to the logical development found in the diagrams of Frege’s Begriffsschrift. Early parts of Begriffsschrift introduce much the same concept of variables and 2/3 of the same tautologies used for the development of propositional logic as Metamath’s main library, set.mm. with the same rule of Modus Ponens.6
Modus Ponens was super-charged by Carew Meredith in the 1950s when he advanced Condensed Detachment which was a version of Modus Ponens where each application required one to unify major and minor premises in the most general way, if possible. So logical proofs based on a small set of axioms could be written in a very concise way which nearly begged for a computer to unwind the terse D-notation proofs into what was actually being proved. Norm Megill was working trying to find the shortest D-notation proofs of various statements when he developed Metamath, a bare bones tool for verifying proofs of theorems which didn’t even have Modus Ponens baked in.
Metamath has the concept of typed metavariables, which can be substituted not just with any value from the applicable domain, but with any valid formula. Thus if 𝑥 ∈ 𝑦 is a valid logical formula, it may be substituted in for a metavariable representing a logical formula. These metavariables are thus a bit slicker than normal variables with some single axioms in metavariables replacing the (infinite) axiom schemata in traditional first order logic. I suppose the thought was that if we needed to go beyond first order logic to apply an axiom schema, why not make that part rigorous7 and foundational. Thus, Metamath allows us to write short, powerful axioms (and rules, like Modus Ponens) which are amenable to mechanical application of substitution without reliance on human language skills and judgment.
And so, a library of human-readable computer-verified theorems has grown over time, with set.mm starting with propositional calculus (i.e. symbolic logic), predicate calculus (symbolic logic over the domain of all sets, with a notion of equality), Zermelo-Fraenkel Set Theory (which tells you which sets are admissible), the Axiom of Choice (which allow you to reason about sets which are hard to describe), and the Tarski–Grothendieck Axiom which says hugely infinite sets exist which lend power to reasoning about problem domains like category theory where merely the uncountable infinite is considered “small.” Sadly, Norm Megill passed away in 2021, but his project continues to be developed.
In this series of posts, I hope to explain how Metamath develops mathematics from these axioms, eventually reaching arithmetic, analysis, topology, geometry, and more. Or you could skip ahead and read up at the project’s website.
Or “Concept Notation: A formula language of pure thought, modelled upon that of arithmetic.”
Although the Begriffsschrift constituted a major advance in logic, it was neither widely understood nor well-received. Some scholars have suggested that this was due to the facts that the notation was 2-dimensional instead of linear and that he didn’t build upon the work of others but rather presented something radically new.
From: Edward N. Zalta, "Gottlob Frege", The Stanford Encyclopedia of Philosophy (Spring 2024 Edition), Edward N. Zalta & Uri Nodelman (eds.), <https://plato.stanford.edu/archives/spr2024/entries/frege/>
As an example, the judgment that exactly one of A or B is true would be written today in shorthand as ⊢ (𝛢 ⊻ 𝛣) but by Frege as possibly
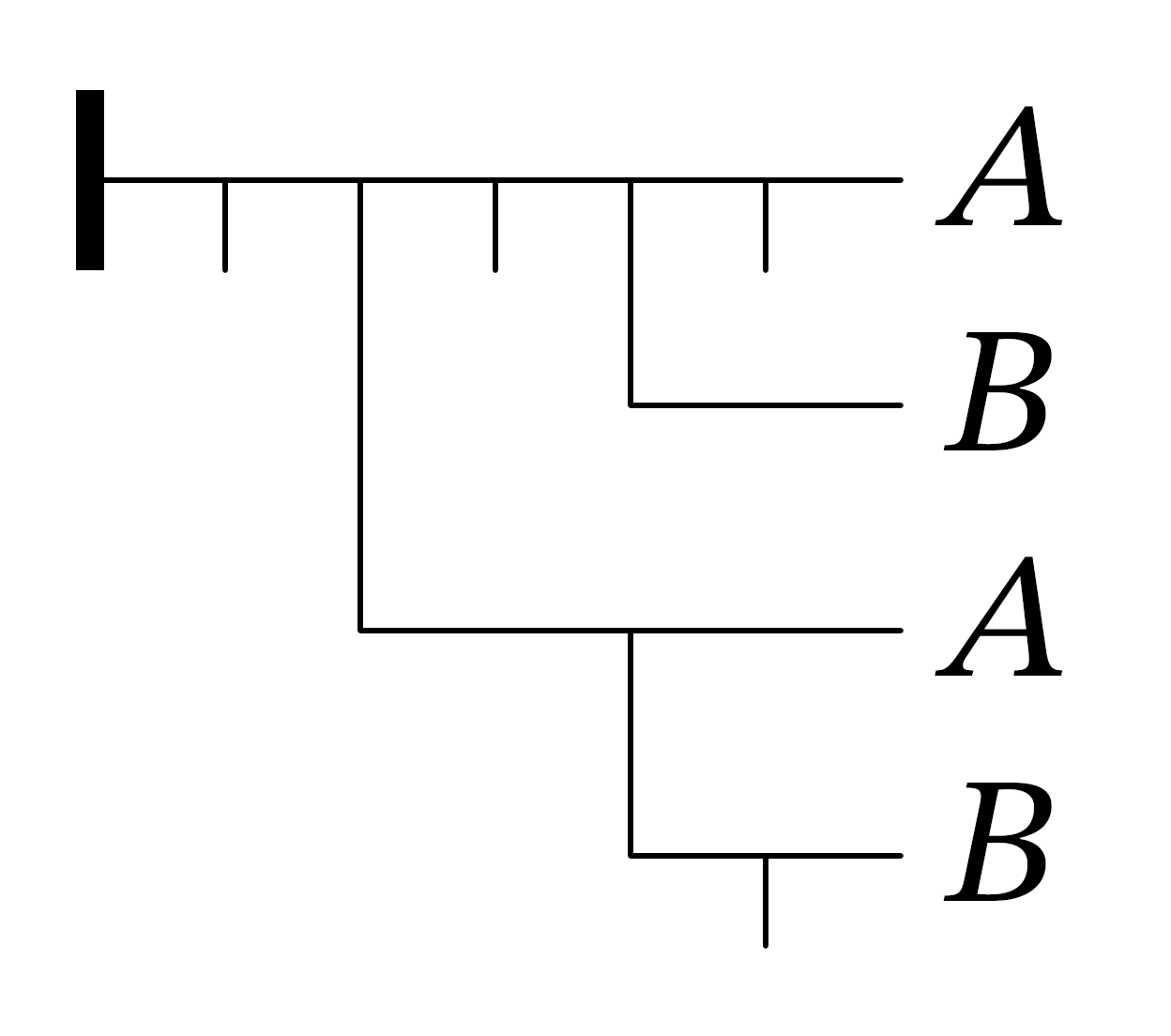
where notation that separates the statement of a judgment from a mere formula, the turnstile, ⊢ , and the negation of forumla, ¬ , persist in today’s symbolic logic.
Native Set Theory treats sets as abstract containers without limit of what they may contain, including possibly themselves. But this abstraction of containers, described in terms of natural language, ultimately admitted contradictions traced to its lax rules.
The fallout resulted in in the realization that if we are to talk rigorously about the concept of a container of objects, not every imagined container can be treated as an object.
This turn-of-the-century revolution not only shook the foundations of mathematics but was happening at roughly the same time as the introduction of Special Relativity and Quantum Mechanics. Symbolically, ⊢ ¬∃𝑥(𝑦 ∈ 𝑥 ↔︎ ¬ 𝑦 ∈𝑦), E² = (m𝑐²)² + (|p|𝑐)², and (E, |p|) = ℎ(f, λ⁻¹) = ℏ(𝜔, |𝑘|) all hit the scientific world at about the same time.
Russell’s Paradox is one of the problems with treating the hypothetical collection of all sets as if it too were a set. For if the collection of all sets is a set, then the collection of all sets which do not contain themselves as an element would be a subset of that set, and therefore definitely a set as well. Call this second set, R. Since R is a set, it is an element of itself if and only if† is is not an element of itself. Most would trace the problem to the assumption that the collection of all sets which do not contain themselves is a set itself. This implies that the collection of all sets cannot be a set. Which implies we need to make some choices of what types of collections can legally be treated as sets admissible to a new formal theory.
Axiomatic Set Theory improves the situation by writing down the rules of what we will choose to consider as a set. These formal rules, written in the language of logic, are called the axioms of our set theory. From the etymology of axiom, we would want all axioms to be self-evident to anyone who studies the field, but even as Euclid’s 5th postulate turns out to be weird, wordy, and not the only possible choice, the axioms of set theory are subject to debate and there are inequivalent competing theories in the literature.
† The expression “if and only if” (frequently abbreviated as iff) signals a bi-implication, as “A iff B” means both “A implies B” and “B implies A”. Symbolically, implication is shown with a right-pointing arrow, →, while bi-implication is shown with an arrow that points both ways, ↔︎ or ⇔.
Metamath refers to a computer-verified proof system which attempts to be free of built-in mathematics, so proofs can be traced in entirety back to their roots and to the library of thousands of theorems built on various foundations. More on this, later.
"Modus ponens" is the rule that if you are given the major premise that the truth of proposition A implies the truth of proposition B, and the minor premise that asserts the truth of proposition A, then it follows that proposition B is true. It is also called “Detachment” as the minor premise, A, is detached from the major premise of “A implies B”, leaving behind the conclusion of B.
One way that they are rigorous is that a statement may specify that some metavariables may not be substituted if they have any terms in common. For example, the truth of a formula for a particular value of 𝑥 does not imply it is true for all values of 𝑥 unless 𝑥 doesn’t actually appear in the formula. So 𝑥 and the formula (or rather all metavariables in the formula) would need to have the distinct variable restriction for this to be a valid rule. These special rules used to be commonly written out in English for the older axiom schemata.




